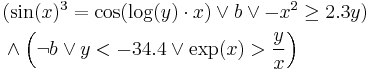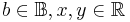Satisfiability Modulo Theories

In computer science, the Satisfiability Modulo Theories (SMT) problem is a decision problem for logical formulas with respect to combinations of background theories expressed in classical first-order logic with equality. Examples of theories typically used in computer science are the theory of real numbers, the theory of integers, and the theories of various data structures such as lists, arrays, bit vectors and so on. SMT can be thought of as a form of the constraint satisfaction problem and thus a certain formalized approach to constraint programming.

Contents

Basic terminology

Formally speaking, an SMT instance is a formula in first-order logic, where some function and predicate symbols have additional interpretations, and SMT is the problem of determining whether such a formula is satisfiable. In other words, imagine an instance of the Boolean satisfiability problem (SAT) in which some of the binary variables are replaced by predicates over a suitable set of non-binary variables. A predicate is basically a binary-valued function of non-binary variables. 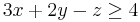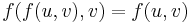Example predicates include linear inequalities (e.g., 3x%2B 2y - z \geq 4) or equalities involving uninterpreted terms and function symbols (e.g., f(f(u, v), v) = f(u, v) where f is some unspecified function of two unspecified arguments.) These predicates are classified according to the theory they belong to. For instance, linear inequalities over real variables are evaluated using the rules of the theory of linear real arithmetic, whereas predicates involving uninterpreted terms and function symbols are evaluated using the rules of the theory of uninterpreted functions with equality (sometimes referred to as the empty theory). Other theories include the theories of arrays and list structures (useful for modeling and verifying software programs), and the theory of bit vectors (useful in modeling and verifying hardware designs). 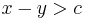Subtheories are also possible: for example, difference logic is a sub-theory of linear arithmetic in which each inequality is restricted to have the form x - y > c for variables x and y and constant c.

Most SMT solvers support only quantifier free fragments of their logics.

Expressive power of SMT

An SMT instance is a generalization of a Boolean SAT instance in which various sets of variables are replaced by predicates from a variety of underlying theories. Obviously, SMT formulas provide a much richer modeling language than is possible with Boolean SAT formulas. For example, an SMT formula allows us to model the datapath operations of a microprocessor at the word rather than the bit level.

By comparison, answer set programming is also based on predicates (more precisely, on atomic sentences created from atomic formula). Unlike SMT, answer-set programs do not have quantifiers, and cannot easily express constraints such as linear arithmetic or difference logic -- ASP is at best suitable for boolean problems that reduce to the free theory of uninterpreted functions. Implementing 32-bit integers as bitvectors in ASP suffers from most of the same problems that early SMT solvers faced: "obvious" identities such as x+y=y+x are difficult to deduce.

Constraint logic programming does provide support for linear arithmetic constraints, but within a completely different theoretical framework.

SMT solvers

Early attempts for solving SMT instances involved translating them to Boolean SAT instances (e.g., a 32-bit integer variable would be encoded by 32 bit variables with appropriate weights and word-level operations such as 'plus' would be replaced by lower-level logic operations on the bits) and passing this formula to a Boolean SAT solver. This approach, which is referred to as the eager approach, has its merits: by pre-processing the SMT formula into an equivalent Boolean SAT formula we can use existing Boolean SAT solvers "as-is" and leverage their performance and capacity improvements over time. On the other hand, the loss of the high-level semantics of the underlying theories means that the Boolean SAT solver has to work a lot harder than necessary to discover "obvious" facts (such as 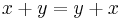x %2B y = y %2B x for integer addition.) This observation led to the development of a number of SMT solvers that tightly integrate the Boolean reasoning of a DPLL-style search with theory-specific solvers (T-solvers) that handle conjunctions (ANDs) of predicates from a given theory. This approach is referred to as the lazy approach.

Dubbed DPLL(T) [1], this architecture gives the responsibility of Boolean reasoning to the DPLL-based SAT solver which, in turn, interacts with a solver for theory T through a well-defined interface. The theory solver need only worry about checking the feasibility of conjunctions of theory predicates passed on to it from the SAT solver as it explores the Boolean search space of the formula. For this integration to work well, however, the theory solver must be able to participate in propagation and conflict analysis, i.e., it must be able to infer new facts from already established facts, as well as to supply succinct explanations of infeasibility when theory conflicts arise. In other words, the theory solver must be incremental and backtrackable.

SMT for undecidable theories

Most of the common SMT approaches support decidable theories. However, many real-world systems can only be modelled by means of non-linear arithmetic over the real numbers involving transcendental functions, e.g. an aircraft and its behavior. This fact motivates an extension of the SMT problem to non-linear theories, e.g. determine whether

\begin{align} & (\sin(x)^3 = \cos(\log(y)\cdot x) \vee b \vee -x^2 \geq 2.3y) \\ & \wedge \left(\neg b \vee y < -34.4 \vee \exp(x) > {y \over x}\right) \end{align}

where

b \in {\mathbb B}, x,y \in {\mathbb R}

is satisfiable. Then, such problems become undecidable in general. (It is important to note, however, that the theory of real closed fields, and thus the full first order theory of the real numbers, are decidable using quantifier elimination. This is due to Alfred Tarski.) The first order theory of the natural numbers with addition (but not multiplication), called Presburger arithmetic, is also decidable. Since multiplication by constants can be implemented as nested additions, the arithmetic in many computer programs can be expressed using Presburger arithmetic, resulting in decidable formulas.

Examples of SMT solvers addressing Boolean combinations of theory atoms from undecidable arithmetic theories over the reals are ABsolver[2], which employs a classical DPLL(T) architecture with a non-linear optimization packet as (necessarily incomplete) subordinate theory solver, and HySAT-2, building on a unification of DPLL SAT-solving and interval constraint propagation called the iSAT algorithm [3].

SMT solvers

The table below summarizes some of the features of the many available SMT solvers. The column "SMT-LIB" indicates compatibility with the SMT-LIB language; many systems marked 'yes' may support only older versions of SMT-LIB, or offer only partial support for the language. The column "CVC" indicates support for the CVC language. The column "DIMACS" indicates support for the DIMACS format.

Projects differ not only in features and performance, but also in the viability of the surrounding community, its ongoing interest in a project, and its ability to contribute documentation, fixes, tests and enhancements. Based on these measures, it appears that the most vibrant, well-organized projects are OpenSMT, STP and CVC4.

Platform Features Notes
Name OS License SMT-LIB CVC DIMACS Built-in theories API SMT-COMP [1]
ABsolver Linux CPL v 1.2 No Yes linear arithmetic, non-linear arithmetic C++ no DPLL-based
Alt-Ergo Linux, Mac OS, Windows Free software v 1.2 empty theory, linear arithmetic OCaml 2008 based on congruence closure
Barcelogic Linux Proprietary v 1.2 empty theory, difference logic C++ 2009 DPLL-based, congruence closure
Beaver Linux, Windows BSD v 1.2 No No bitvectors OCaml 2009 SAT-solver based
Boolector Linux GPLv3 v 1.2 No No bitvectors, arrays C 2009 SAT-solver based
CVC3 Linux BSD v 1.2 Yes empty theory, linear arithmetic, arrays, tuples, types, records, bitvectors, quantifiers C/C++ 2010 proof output to HOL
CVC4 Linux BSD Yes pre-alpha 2010 active development; pre-alpha
Decision Procedure Toolkit (DPT) Linux Apache No OCaml no DPLL-based
iSAT Linux Proprietary No non-linear arithmetic no DPLL-based
MathSAT Linux Proprietary partial v2.0 empty theory, difference logics, linear arithmetic 2010 DPLL-based
MiniSmt Linux LGPL partial v2.0 non-linear arithmetic 2010 Yices-based
OpenSMT Linux GPLv3 partial v2.0 Yes empty theory, differences, linear arithmetic, bitvectors C++ 2010 lazy SMT Solver
SatEEn  ? Proprietary v 1.2 linear arithmetic, difference logic none 2009
SONOLAR Linux, Windows Proprietary partial v2.0 bitvectors C 2010 SAT-solver based
Spear Linux, Mac OS, Windows Proprietary v 1.2 bitvectors 2008
STP Linux, OpenBSD, Windows, Mac OS MIT partial v2.0 Yes No bitvectors, arrays C, C++, Python, OCaml, Java 2010 SAT-solver based
SWORD Linux Proprietary v 1.2 bitvectors 2009
UCLID Linux BSD No No No empty theory, linear arithmetic, bitvectors, and constrained lambda (arrays, memories, cache, etc.) no SAT-solver based, written in Moscow ML. Input language is SMV model checker. Well-documented!
veriT Linux BSD partial v2.0 empty theory, difference logic C/C++ 2010 SAT-solver based
Yices Linux, Mac OS, Windows Proprietary v 1.2 2009
Z3 Linux, Windows Proprietary partial v2.0 empty theory, linear arithmetic, bitvectors, arrays, quantifiers C, .Net, OCaml 2008

See also

Notes

  1. ^ Nieuwenhuis, R.; Oliveras, A.; Tinelli, C. (2006), "Solving SAT and SAT Modulo Theories: From an Abstract Davis-Putnam-Logemann-Loveland Procedure to DPLL(T)", Journal of the ACM, 53, pp. 937–977., ftp://ftp.cs.uiowa.edu/pub/tinelli/papers/NieOT-JACM-06.pdf 
  2. ^ Bauer, A.; Pister, M.; Tautschnig, M. (2007), "Tool-support for the analysis of hybrid systems and models", Proceedings of the 2007 Conference on Design, Automation and Test in Europe (DATE'07), IEEE Computer Society, p. 1, doi:10.1109/DATE.2007.364411 
  3. ^ Fränzle, M.; Herde, C.; Ratschan, S.; Schubert, T.; Teige, T. (2007), "Efficient Solving of Large Non-linear Arithmetic Constraint Systems with Complex Boolean Structure", JSAT Special Issue on SAT/CP Integration, 1, pp. 209–236, http://jsat.ewi.tudelft.nl/content/volume1/JSAT1_11_Fraenzle.pdf 

References

This article is adapted from a column in the ACM SIGDA e-newsletter by Prof. Karem Sakallah. Original text is available here